Distance Between Sines
Proposition
Let $\alpha > \beta > 0$ be two distinct real numbers. Then
\[\begin{align} \sup _{x \in \mathbb R} |\sin (\alpha x) - \sin (\beta x)| \ge \sqrt 3. \end{align}\]Proof.
\[\begin{align*} \sin (\alpha x) - \sin (\beta x) &= 2 \cos \left( \frac{\alpha + \beta}2 x \right) \sin \left( \frac{\alpha - \beta}2 x \right). \end{align*}\]Whenever $x = \dfrac{2 k \pi}{\alpha + \beta}$, $\left|\cos \left( \dfrac{\alpha + \beta}2 x \right)\right| = 1$, so
\[\begin{align*} \sin (\alpha x) - \sin (\beta x) &= \pm 2 \sin \left( \frac{\alpha - \beta}2 \frac{2 k \pi}{\alpha + \beta} \right) \\\ &= \pm 2 \sin \left( \frac{\alpha - \beta}{\alpha + \beta} k \pi \right) \end{align*}\]Let $\gamma = \dfrac{\alpha - \beta}{\alpha + \beta}$. If $\gamma$ is an irrational number, then $\sup _k \sin (\gamma k \pi) = 1$ (see Stein, Fourier Analysis for example). If $\gamma$ is a rational number, then the set $\lbrace\gamma k\rbrace$ mod 1 will be $\lbrace 0, \frac1q, \frac2q, \dots, \frac{q-1}q \rbrace$ for some $q$, which must contain an element in $[\frac13, \frac23]$, so $\lvert\sin (\gamma k \pi)\rvert \ge \frac{\sqrt 3}2$ for some $k$.
Comment.
$\sqrt 3$ is not optimal. By a rescaling in $x$, we may assume that $\beta = 1$. $\gamma$ will be exactly $\frac13$ when $\alpha = 2$, and $\gamma$ will be $\frac23$ when $\alpha = 5$. In the case $\alpha = 2$,
\[\begin{align*} f (x) := \sin (2 x) - \sin (x) \end{align*}\]is smooth and periodic over $\mathbb R$. To find its critical points, set
\[\begin{align*} f' (x) = 2 \cos (2 x) - \cos (x) &= 0. \\\ 4 \cos (x) ^2 - 2 - \cos (x) &= 0. \\\ \cos (x) &= \frac{1 \pm \sqrt{33}}8. \end{align*}\]Because $f$ is odd, it suffices to consider $x \in (0, \pi)$. When
\[\begin{align*} x &= \cos ^{-1} \left( \frac{1 + \sqrt{33}}8 \right) \\\ \sin (x) &= \sqrt{1 - \cos ^2 (x)} \\\ &= \sqrt{1 - \frac{(1 + \sqrt{33})^2}{64}} \\\ &= \sqrt{1 - \frac{34 + 2 \sqrt{33}}{64}} \\\ &= \frac18 \sqrt{30 - 2 \sqrt{33}} \\\ f (x) &= 2 \sin (x) \cos (x) - \sin (x) \\\ &= \left(\frac{1 + \sqrt{33}}4 - 1\right) \frac18 \sqrt{30 - 2 \sqrt{33}} \approx 0.3690. \end{align*}\]When
\[\begin{align*} x &= \cos ^{-1} \left( \frac{1 - \sqrt{33}}8 \right) \\\ \sin (x) &= \sqrt{1 - \cos ^2 (x)} \\\ &= \sqrt{1 - \frac{(1 - \sqrt{33})^2}{64}} \\\ &= \sqrt{1 - \frac{34 - 2 \sqrt{33}}{64}} \\\ &= \frac18 \sqrt{30 + 2 \sqrt{33}} \\\ f (x) &= 2 \sin (x) \cos (x) - \sin (x) \\\ &= \left(\frac{1 - \sqrt{33}}4 - 1\right) \frac18 \sqrt{30 + 2 \sqrt{33}} \approx -1.7602. \end{align*}\]Therefore
\[\begin{align*} \sup _{x} |\sin(2 x) - \sin (x)| \approx 1.7602. \end{align*}\]In the case $\alpha = 5$,
\[\begin{align*} g (x) := \sin (5 x) - \sin (x) \end{align*}\]is smooth and periodic over $\mathbb R$. To find its critical points, set
\[\begin{align*} g' (x) = 5 \cos (5 x) - \cos (x) &= 0. \\\ 5 \cos ^5 x - 50 \cos ^3 x \sin ^2 x + 25 \cos x \sin ^4 x - \cos (x) &= 0. \\\ \cos (x) \left[ 5 \cos ^4 x - 50 \cos ^2 x (1 - \cos ^2 x) + 25 (1 - \cos ^2 x) ^2 - 1 \right] &= 0. \\\ 4 \cos (x) \left[ 20 \cos ^4 x - 25 \cos ^2 x + 6 \right] &= 0. \\\ \cos (x) = 0 \qquad \text{ or } \qquad \cos ^2 (x) = \frac{25 \pm \sqrt{145}}{40}. \end{align*}\]Notice that
\[\begin{align*} g (x) = 4 \sin x (4 \cos ^4 x - 3 \cos ^2 x). \end{align*}\]If $\cos x = 0$ then $g (x) = 0$. If $\cos ^2 x = \frac{25 \pm \sqrt{145}}{40}$ then $20 \cos ^4 x - 25 \cos ^2 x + 6 = 0$. So
\[\begin{align*} g (x) &= 4 \sin x (4 \cos ^4 x - 3 \cos ^2 x) \\\ &= 4 \sin x \left(5 \cos ^2 x - \frac65 - 3 \cos ^2 x\right) \\\ &= \frac85 \sin x \left(5 \cos ^2 x - 3\right) \end{align*}\]Because $f$ is odd and of period $\pi$, it suffices to consider $x \in (0, \frac\pi2)$. When
\[\begin{align*} x &= \cos ^{-1} \left(\sqrt{\frac{25 + \sqrt{145}}{40}}\right) \\\ \sin x &= \sqrt{1 - \frac{25 + \sqrt{145}}{40}} \\\ &= \sqrt{\frac{15 - \sqrt{145}}{40}} \\\ g (x) &= \frac85 \sqrt{\frac{15 - \sqrt{145}}{40}} \left(5 \frac{25 + \sqrt{145}}{40} - 3\right) \approx 0.7093. \end{align*}\]When
\[\begin{align*} x &= \cos ^{-1} \left(\sqrt{\frac{25 - \sqrt{145}}{40}}\right) \\\ \sin x &= \sqrt{1 - \frac{25 - \sqrt{145}}{40}} \\\ &= \sqrt{\frac{15 + \sqrt{145}}{40}} \\\ g (x) &= \frac85 \sqrt{\frac{15 + \sqrt{145}}{40}} \left(5 \frac{25 - \sqrt{145}}{40} - 3\right) \approx -1.8157. \end{align*}\]Therefore
\[\begin{align*} \sup _{x} |\sin(5 x) - \sin (x)| \approx 1.8157. \end{align*}\]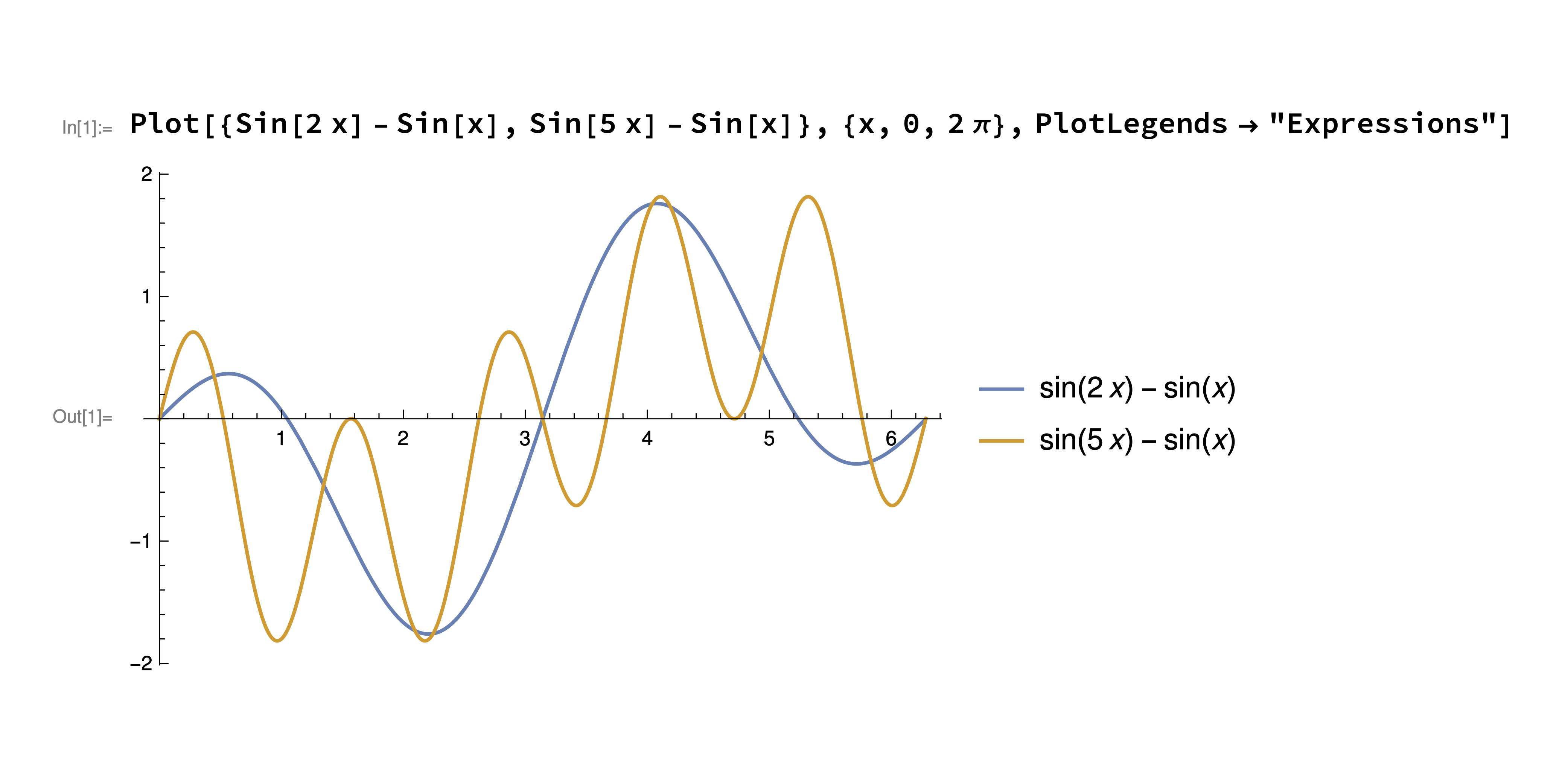
For any other $\alpha$, $\lbrace\gamma k\rbrace \operatorname{mod} 1 = \lbrace 0, \frac1q, \frac2q, \dots, \frac{q-1}q \rbrace$ for some $q \neq 3$, which must contain an element in $[\frac25, \frac35]$, so $\lvert\sin (\gamma k \pi)\rvert \ge \sin\left(\dfrac{5\pi}2\right) = \sqrt{\dfrac58+\dfrac{\sqrt5}8} \approx 0.9511$ for some $k$. To sum up, for $\alpha > \beta > 0$,
\[\begin{align*} \sup _{x \in \mathbb R} |\sin (\alpha x) - \sin (\beta x)| \begin{cases} \approx 1.7602 & \alpha = 2 \beta \\ \approx 1.8157 & \alpha = 5 \beta \\ \ge 1.9021 & \frac\alpha\beta \in \mathbb Q \setminus \lbrace 2, 5 \rbrace \\ = 2 & \frac\alpha\beta \in \mathbb R \setminus \mathbb Q \end{cases} . \end{align*}\]